a illustrative sketch of the infinite slope model representing the
Table of Contents
Table of Contents
If you’re a student or a professional in the field of mathematics, you know how important it is to understand how to draw a slope. The ability to draw a slope is crucial in many mathematical applications, including graphing, trigonometry, and calculus. In this article, we will explore the different techniques and tips for drawing a slope that will help you improve your mathematical skills and make your calculations more accurate and precise.
It can be challenging to understand the concept of drawing a slope, especially for those who are new to the field of mathematics. Many students struggle to understand the different techniques and formulas required to draw an accurate slope. Moreover, it can be challenging to comprehend the geometric shapes that form the slope, which can result in incorrect calculations and a lack of confidence in your mathematical abilities.
If you want to learn how to draw a slope, it’s essential to understand the basic concept behind this mathematical operation. A slope, in its simplest form, represents the steepness or incline of a line. Drawing a slope requires you to calculate the change in the Y-axis over the change in the X-axis, which results in a value called the slope coefficient.
In this article, we have explored the basics of drawing a slope and provided some essential tips to help you improve your calculation accuracy. We have discussed the importance of understanding the concept of the slope and the different techniques used to calculate its value.
How to Draw a Slope and Its Target
The target of drawing a slope is to calculate the change in the Y-axis over the change in the X-axis, which results in a value called the slope coefficient. Drawing a slope is a straightforward process that involves plotting two points on a Cartesian plane and calculating the slope coefficient.
When I was in college, I struggled with understanding how to draw a slope. However, with the help of my professors and some online resources, I was able to grasp the concept and improve my mathematical skills. One of the essential tips I learned is that it’s crucial to plot the points accurately, as even a slight mistake can result in incorrect calculations.
 After plotting the points, the next step is to calculate the slope coefficient by using the formula (y2-y1)/(x2-x1). Once you have obtained the slope coefficient, you can use it to draw the slope on the Cartesian plane. Remember that the slope represents the steepness or incline of the line and can have a positive, negative, or zero value.
After plotting the points, the next step is to calculate the slope coefficient by using the formula (y2-y1)/(x2-x1). Once you have obtained the slope coefficient, you can use it to draw the slope on the Cartesian plane. Remember that the slope represents the steepness or incline of the line and can have a positive, negative, or zero value.
Tips for Drawing a Slope
One of the most critical tips for drawing a slope is to ensure that you plot the points accurately. Even a slight mistake can result in incorrect calculations and a lack of confidence in your mathematical skills. Additionally, it’s essential to understand the concept of the slope and the different techniques used to calculate its value.
Use of Slope Charts
Slope charts are an essential tool for drawing a slope, especially in complex mathematical calculations. They help you visualize the slope as a geometric shape and provide a visual representation that can make the calculations more comfortable and more accurate. They can be created using different software applications, including Power BI and GeoGebra.
Practice Makes Perfect
Like any other mathematical operation, the key to mastering how to draw a slope is practice. The more you practice, the more comfortable and confident you will become in applying the different techniques and formulas required to draw an accurate slope.
Question and Answer
Q1: What is the importance of drawing a slope?
A1: The ability to draw a slope is crucial in many mathematical applications, including graphing, trigonometry, and calculus. The slope is used to represent the steepness or incline of a line and can have a positive, negative, or zero value.
Q2: What is the formula for calculating the slope coefficient?
A2: The formula for calculating the slope coefficient is (y2-y1)/(x2-x1), where y1, y2, x1, and x2 are the values of the two points on the line.
Q3: What are slope charts?
A3: Slope charts are visual representations of the slope as a geometric shape that can be created using different software applications, including Power BI and GeoGebra. They help you visualize the slope and make the calculations more comfortable and more accurate.
Q4: What is the importance of plotting the points accurately when drawing a slope?
A4: Plotting the points accurately is essential when drawing a slope, as even a slight mistake can result in incorrect calculations and a lack of confidence in your mathematical skills.
Conclusion of How to Draw a Slope
Drawing a slope is an essential skill that is required in many mathematical applications. It’s essential to understand the concept of the slope and the different techniques used to calculate its value. With the tips and techniques discussed in this article, you can improve your mathematical skills and draw an accurate slope with ease. Remember that practice makes perfect, and the more you practice, the more confident and comfortable you will become in applying the different formulas and techniques required to draw a slope accurately.
Gallery
Slope Drawings RECPs
-With Border.jpg)
Photo Credit by: bing.com /
(a) Illustrative Sketch Of The Infinite Slope Model Representing The

Photo Credit by: bing.com / slope illustrative representing slopes
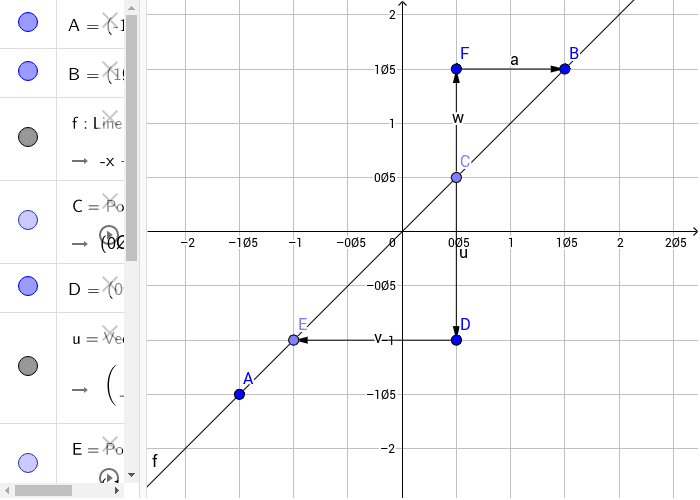
Draw A Slope Triangle For The Line. – GeoGebra

Photo Credit by: bing.com / geogebra
[Solved] How To Draw Slope Fields With All The Possible | 9to5Science
![[Solved] How to draw slope fields with all the possible | 9to5Science [Solved] How to draw slope fields with all the possible | 9to5Science](https://i.stack.imgur.com/lpKQA.png)
Photo Credit by: bing.com /
Draw Slope Chart In Power BI: Part 8 | RADACAD
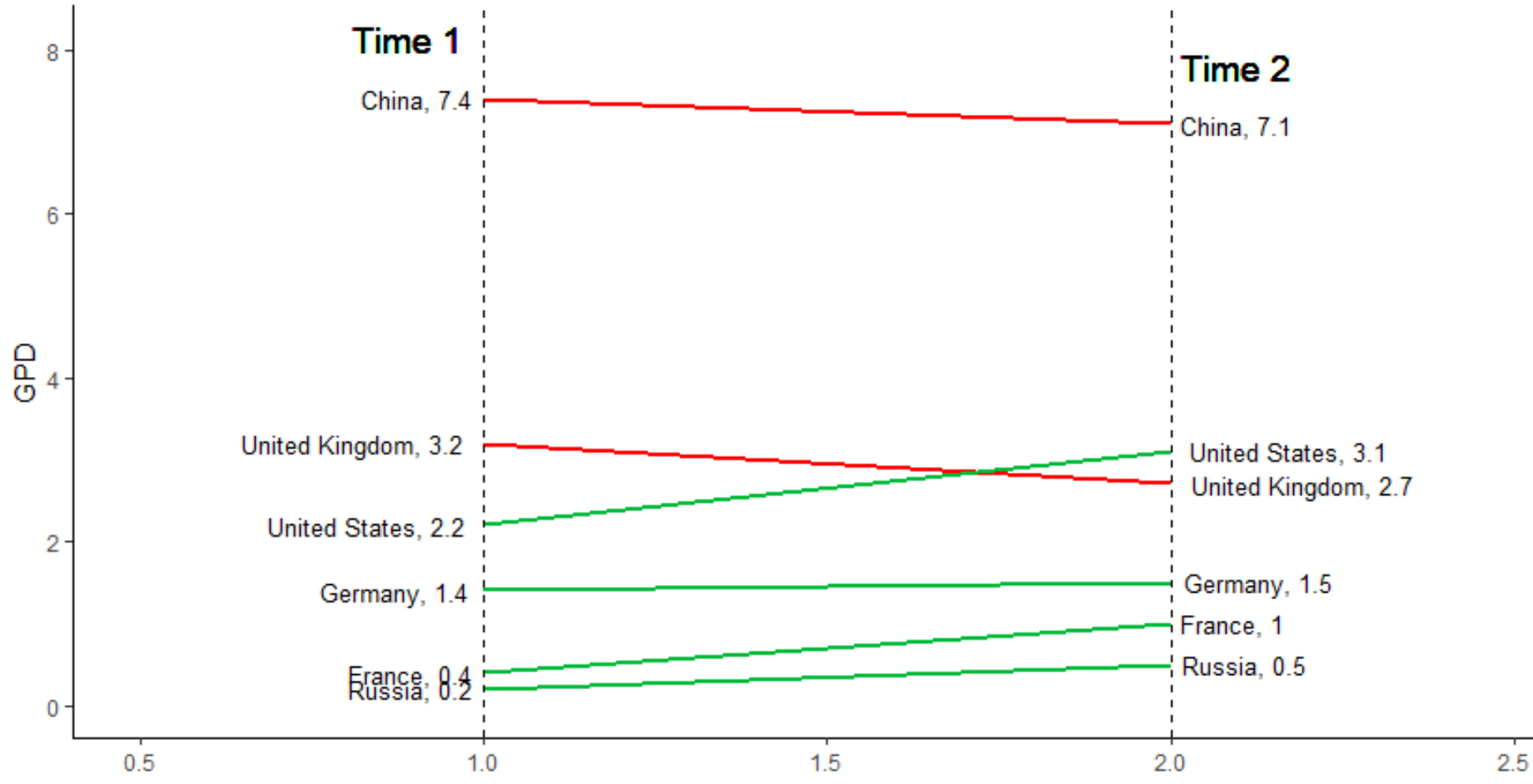
Photo Credit by: bing.com / slope chart power bi draw part radacad slopechart





